按:原文见 《社会》官网,2017年第2期。代码及数据在此处。
题图致敬 DGG、Linton Freeman、R. Breiger。
导言
随着互联网和智能设备愈来愈多的介入人们的日常生活以及大数据概念的提出,在社会科学研究领域,研究者们面临一个新的非常巨大的数据源。不同于传统的问卷调查数据,这个新的数据源来自于各类智能设备所记录的数据,例如手机信号塔所记录的在某个范围内的人群聚集、摄像头所捕捉到的人们在各个场所的出席、人们在互联网使用过程中所留下的轨迹或积累的信息,例如在微博上面的评论或转发,在网络论坛的发帖和回帖。也有一些数据早已进入研究者的视野,但是由于信息化手段的丰富,研究者们无需再大费周章专门进行数据录入或转换,例如人们的日常消费记录、学术文献的作者信息和引文信息、公司间的联动交易行为等等。对于上述这类数据,研究者们往往关注其中的共现关系,并探讨其潜在的社会机制。例如共同在一个论坛帖子里进行讨论的用户可能具有相同的兴趣话题,在科学文献作品中科学家之间如何形成合作关系,图书购买记录背后所蕴含的共同的政治态度和价值观等等。
一般来说,对上述数据的分析大多采用社会网络分析方法进行。从数据分析的角度,这类互动数据可以采用一个发生矩阵(incidence matrix)来表示,例如一个$n \times m$的二进制矩阵$P$,其中矩阵的行表示某个场所或事件,例如微博的博文,学术文章或者购物清单等等,矩阵的列则表示参与该事件的基本单位或成员,例如转发微博的用户、文章作者或者购物商品名称。若 $p_{\text{ij}} = 1$ 则表示第 $j$ 个成员参与了第 $i$ 次事件,反之则表示没有参与。矩阵 $P$ 也可以采用权值的方式表示,即矩阵元素的取值表示参与的权值,例如回帖或转发的次数、所购买的商品数量、停留的时长等等。

在社会网络分析方法中,将上述社会网络结构称为双模网络,又称双重网络 (bipartite)或"隶属网"。
对双模数据的分析方法已经有很多,既有直接对双模网络的关联模式进行分析的方法,也有采用降模法将双模网络变为单模网络的分析方法。对于行为观测数据而言,研究者通常只关心参与者这个模所潜在的社会网络模式,事件模通常作为协变量来考虑。将二进制双模数据做一个简单的矩阵映射,就可得到一个单模矩阵,又称共生矩阵(co-occurrence matrix)。这个单模矩阵既可以是表示列模的数据($P^{T} \times P$,$m \times m$),也可以是表示行模的数据($P \times P^{T}$,$n \times n$),取决于研究者的需要。单模矩阵的数值则表示参与者两两之间共同出现的频次,因此该矩阵可视为有权网。从计算的角度来说,使用矩阵映射进行降模可以得到参与者的行为频次信息,因此非常简单高效。
然而对于带权值的发生矩阵,降模映射则不太适用。并且,其最大的缺点在于降模之后所得到的是一个密集矩阵。在原双模网络中,若节点的中心度为d的话,则降模之后变为$(d \times (d - 1)/2$,从而放大了网络密度,并在某种程度上扭曲网络结构(Latapy & Magnien et al., 2008)。因此,通常来说还需进一步处理,将其转换为二进制以作为社会网络关系的量度。然而,这种二值化量度,其麻烦在于如何确定阈值。若采用一个单一阈值对矩阵权值进行转换,则其潜在假设是参与者有相同的分布。举个例子,在网络社区中,网络成员之间的发帖数和回复数存在非常大的变差。假设成员 $x$ 与 $z$ 共有3次回复,成员 $y$ 与 $z$ 共有5次回复,但$x$的总回帖量是3次,而$y$的总回帖量是100次。我们该如何判定或比较x-z和y-z这两对关系呢?显而易见,基于单一阈值的二值化网络测度难以处理此类情形。在此基础上,可以考虑相对比例,例如3/3与5/100,巴拉特等人就分别提出改进型的加权方案(Barrat & Barthélemy et al., 2004; Newman, 2004; Barthélemy & Barrat et al., 2005),但其重点往往在于探测网络的社区结构,而非节点间的关系测度。
除了降模映射法,典型的方式包括直接计算列模的相关系数矩阵并作为社会网络测量。相关系数法的优点在于能够控制不同参与者的活跃程度,但无法识别虚假相关,同时相关系数矩阵作为一个稠密矩阵也不太适合作为大规模网络的测量。也有学者将双模数据当作"购物篮"问题,采用数据挖掘手段来发现列模之间的关联模式(Raeder & Chawla, 2011; Zweig & Kaufmann, 2011),然而其可信度和解释力不太能够得到保证。
在过去十几年中,在许多学科中,特别是在生物学(Friedman & Linial et al., 2000)、基因学(Ghazalpour & Doss et al., 2006)、神经科学(Huang & Li et al., 2010)等领域,图模型已经成为非常流行的对复杂系统进行抽象,并获得关于大规模观测变量的关联模式的一种处理手段。相比起前述的所介绍的降模映射法、相关系数法等处理方法而言,图模型的计算结果除了避免了前述几种处理方法的缺点之外,能够较好地探测出真实网络结构特征,还具有可解释性强、扩展性高的特点,在面对不同问题时能够展现出强大的解决能力。然而在社会科学领域,相关的研究尚不多见,仅有个别学者用图模型研究美国参议院投票网络、在线论坛发帖网络(陈华珊, 2015)等。相比起图模型在自然科学领域应用的流行性,社会科学领域对它的认识和使用还非常粗浅。在此,本文尝试对图模型进行一番引介,以期引起社会科学界同仁重视,并推动相关研究与应用。
高斯图模型
高斯图模型的基本形式
将观测数据的发生矩阵用一个$n \times p$的矩阵$X$来表示,$n$为观测数,$p$为变量数,假设观测之间相互独立,且$X$为多元正态分布随机变量,
$$X = (X_{1},...,X_{p}) \sim N(\mu,\Sigma)\backslash n$$
在此,对矩阵$X$中节点的两两关系的估计,也称为"邻域选择"(neighborhood selection),其实质是协方差选择问题。邻域选择的目的是对于给定的$n$个i.i.d观测$X$,分别估计每个变量(节点)的相邻变量。即对于集合$\Gamma$中的一个节点$a$,$a \in \Gamma$,它的邻域变量集合用 $X_{ne_{a}}$ 表示,邻域选择的目标是让 $X_{ne_{a}}$ 成为 $\Gamma\backslash{ a}$ 的一个最小子集,使得对于给定的 $X_{ne_{a}}$,$X_{a}$ 条件独立于所有其它变量。从而邻域选择可以被转化为标准的回归问题并求解。
但在数学求解上,一般不直接计算协方差矩阵,而是估计其逆协方差矩阵。这是因为逆协方差矩阵具有独特的性质。假设一个从多元正态分布中独立抽取的$n$个样本,其协方差矩阵为$\Sigma$,则表征样本变量之间条件依赖关系的高斯图模型可由逆协方差矩阵$\Theta = \Sigma^{- 1}$来表示。首先,逆协方差矩阵$\Theta$与协方差矩阵$\Sigma$具有对偶性,由于协方差矩阵为正定矩阵,那么逆协方差矩阵也为正定矩阵,因此它们互为对偶范数(dual norm)。其次,逆协方差矩阵具有稀疏的特质(Mardia & Kent et al., 1980; Lauritzen, 1996),也就是说,当且仅当$\Sigma_{\text{ij}}^{- 1} = 0$时,变量$i$与变量$j$条件独立,反之,变量$i$与变量$j$存在条件依赖关系。逆协方差矩阵在图模型中又称"精度矩阵"(Precision Matrix)或"聚集矩阵"(Concentration Matrix)。
图:逆协方差矩阵与协方差矩阵示例
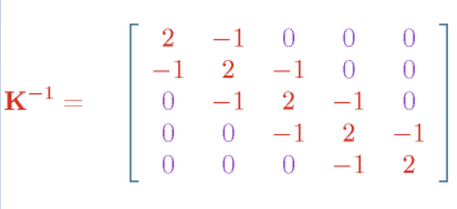
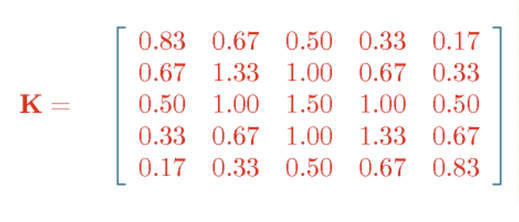
$\Theta$矩阵与偏相关系数有如下关系:
$$\rho_{ij \mid { i,j}} = - \frac{\omega_{\text{ij}}}{\sqrt{\omega_{\text{ii}}\omega_{\text{jj}}}}$$
对于社会关系网络测量来说,当该偏相关系数矩阵的元素大于0,即表示所对应的两个网络节点之间存在联带关系,且该数值可表示联带关系的强弱;反之则不存在联带关系。因此,根据观测数据$X$,计算的步骤为:估计其样本逆协方差矩阵,再转换为偏相关系数矩阵,就可得到该网络的关系测度。
一般采用最大似然法来估计"精度矩阵"$\Sigma^{- 1}$。用$S$表示$X$的经验协方差矩阵,高斯对数最大似然的公式表达如下:
$$\text{log\ }\text{det\ Θ} - trace(\text{SΘ})$$ (1)
其中 $\Theta$ 表示逆协方差矩阵,即 $\Theta = \Sigma^{- 1}$。使公式一最大化可得最大似然估计$\widehat{\Theta} = S^{- 1}$。但是对于大规模观测数据来说,存在两个基本特征:1、高维性。社会网络数据通常包含大量的节点(变量),用矩阵表示的话就是变量数$p$大于观测数$n$,在此情况下,经验协方差矩阵S为奇异矩阵,并不可逆,从而无法估计$\Theta$矩阵。即使 $p \approx n$ ,并且$S$不为奇异矩阵,$\Theta$ 的最大似然估计也会由于过高的方差从而失去效力;2、稀疏性。用图模型所表示的社会网络数据,存在大量的两两条件独立变量,即 $\Theta$ 中存在很多0元素。而根据使公式一最大化所估计得到的 $\text{Θ\ }$一般来说不存在值为0的元素。基于这两个性质,样本协方差矩阵不可逆,估计逆协方差矩阵时存在不稳定、计算成本高和不精确等问题。
罚似然估计法
罚似然估计法
近几十年来,统计学家针对高维稀疏数据提出了很多解决方案,其中蒂施莱尼所提出的罚似然回归法(Tibshirani, 1996)取得了主流地位,并被其它研究者进一步扩展和引进到图模型中(Meinshausen & Bühlmann, 2006; Yuan & Lin, 2007; Peng & Wang et al., 2009)。罚似然法是在线性回归公式中引入一个约束项 (regularizer)或惩罚项(penalty term)$\Theta$,并由一个非负的优化参数(tuning parameter) $\lambda$来控制,当 $\lambda$ 足够大时,$\Theta$的一些元素的值将等于零,也就是说 $\lambda$ 值越大,所估计的逆协方差矩阵越稀疏。并且,即使在 $p \gg n$ 的情形下,公式仍然能够求解,其表达式如下:
$$\text{maximiz}e_{\Theta}{ log\text{detΘ} - trace(\text{SΘ}) - \lambda \mid \mid \Theta \mid \mid_{1}}$$
其中,$\mid \mid \Theta \mid \mid_{1}$ 为 $l_{1}$ 罚则,表示对矩阵$\Theta$的所有元素的绝对值求和。将公式二用社会统计学教材常用的残差最小化拟合公式写法来表示,就是将:
$$RSS=\sum_{i=1}^{n}(y_i - \beta_0 - \sum_{j=1}^{p}\beta_jx_{ij})^2$$
改写为:
$$RSS + \lambda \sum_{j=1}^{p} |(\beta_j)|$$
在上式中,当$\lambda = 0$时,即为常规的OLS回归残差项。由于$\lambda$非负,因此当整个回归模型保留的变量越多,残差惩罚越大,反之则残差惩罚越小,从而$\lambda$作为模型超参数能够控制模型中所保留变量的稀疏程度。
梅豪森和布尔曼最早将罚似然回归应用到图模型中(Meinshausen & Bühlmann, 2006),他们实际上是将网络的每一个节点作为因变量,其它所有节点作为自变量来构建一系列($p$个)回归方程,从而得到一个近似解。其后,许多研究者提出了不同的求解法。有的学者借用万德伯格等人所提出的"内点搜索法"(interior-point)(Vandenberghe & Boyd et al., 1998)进行求解(Yuan & Lin, 2007)。贝纳杰等人则提出用"分块坐标递降法"(blockwise coordinate descent approach)来求解(Banerjee & El Ghaoui et al., 2008),弗里德曼和哈斯蒂等人在此基础上进一步提出用坐标递降法(coordinate descent procedure)来求解(Friedman & Hastie et al., 2008),并证明,当$p>n$的时候,坐标递降法具有很高的计算效率。
所有采用罚则对图模型进行稀疏求解的算法都可被称为图形罚极大似然法或罚似然图模型(以下简称glasso或图模型)。glasso模型近年来在基因研究、流行病学等领域有了很多应用研究,并且模型进一步从单一高斯图模型扩展成动态图模型(Ahmed & Xing, 2009; Song & Kolar et al., 2009)、多组图模型(Guo & Levina et al., 2011; Danaher & Wang et al., 2014)以及多层次图模型和潜变量图模型(Ambroise & Chiquet et al., 2009; Chandrasekaran & Parrilo et al., 2012)等。本文将在第二节展开介绍扩展模型。
最优参数选择与模型评估
在公式二中,参数$\lambda$未知,且无法通过样本数据进行推断,因此$\lambda$也称为超参数(hyper parameter),一般采用穷举法(对于多个超参数则可使用网格搜索(Grid Search)等方法)进行搜索。为了更好地评估模型以及避免模型的过度拟合,在机器学习理论中,一般采用交叉验证(Cross Validation)的方式来进行,即将样本数据集分为训练集和测试集,前者用以建立模型,后者则用来评估模型对未知样本进行预测时的精确度。也有学者采用贝叶斯信息准则(BIC)来评估模型,并针对稀疏约束的特点提出扩展贝叶斯信息准则(eBIC)(Chen & Chen, 2008; Foygel & Drton, 2010)。
应用与示例
在社会科学领域,最为著名的数据集恐怕要算美国南方黑人妇女数据集以下简称DGG),该数据集被很多研究者所使用(Freeman, 2003; Neal, 2013)。该数据由人类学家戴维斯和加纳等人使用访谈、观察记录、访客名单以及报纸记载来收集社区妇女参与社区活动的信息。他们的数据包括18名参与者,14次社会事件。研究者们用他们的人类学观察直觉及经验洞察力对这些妇女的社会网络进行了归纳,把她们分成两个子群体,并且在每个组中区分出核心成员、主要成员和边缘成员三个层次。在他们汇报的结果中,编号1至编号8的妇女被分到第一组,其中编号1、2、3、4被称为核心成员,编号5、6、7为主要成员,编号8为边缘成员。编号10到18被归为第二组,其中编号13、14、15是核心成员,11、12为主要成员,编号10、16、17、18为边缘成员。编号9被标识为同时属于两个组,且都作为边缘成员。
表1 美国南方妇女社会活动日常参与记录数据(原始版):
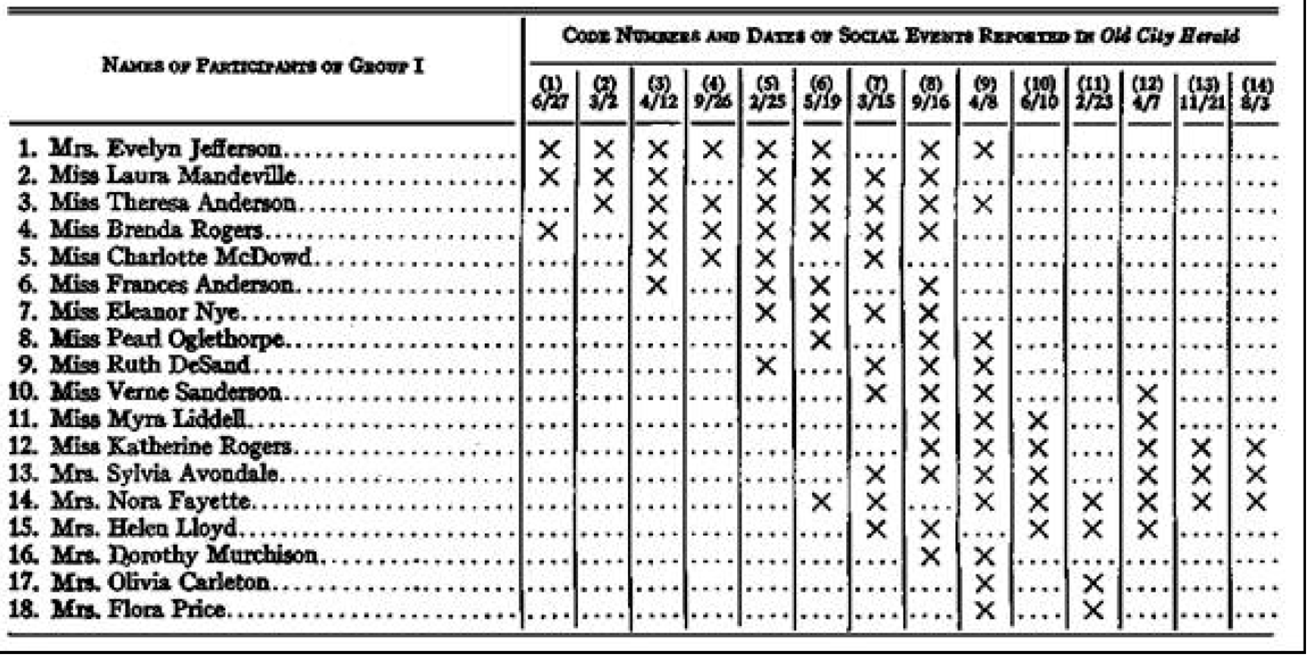
表1.1 美国南方妇女社会活动日常参与记录数据(整理版):

数据来源: (Davis & Gardner et al., 1941)
根据罚似然图模型计算结果,可有两种方式来构建社会关系网络矩阵。方式一为根据所估计的样本逆协方差矩阵,将非零元素转换为1,就可得到常规的社会关系网络表示矩阵,用这种测量方式所得到的网络为无向网络。方式二为根据样本逆协方差矩阵进一步计算偏相关系数矩阵,作为社会关系网络的测量,其中偏相关系数可作为关系的权重,由此,可得到无向有权网络(undirected valued network)。在实际应用中,上述方式所得到的关系矩阵很可能不是对称矩阵,还需做对称化处理。对于样本逆协方差矩阵可采用"或法则"(OR rule,即矩阵中每一对对角元素若任一个值不等于零则视为存在条件依赖)或"且法则"(AND rule,每一对对角元素均不等于零才视为存在条件依赖);对于偏相关系数矩阵则可对每一对对角元素求平均值、最大值或最小值等方式来处理。
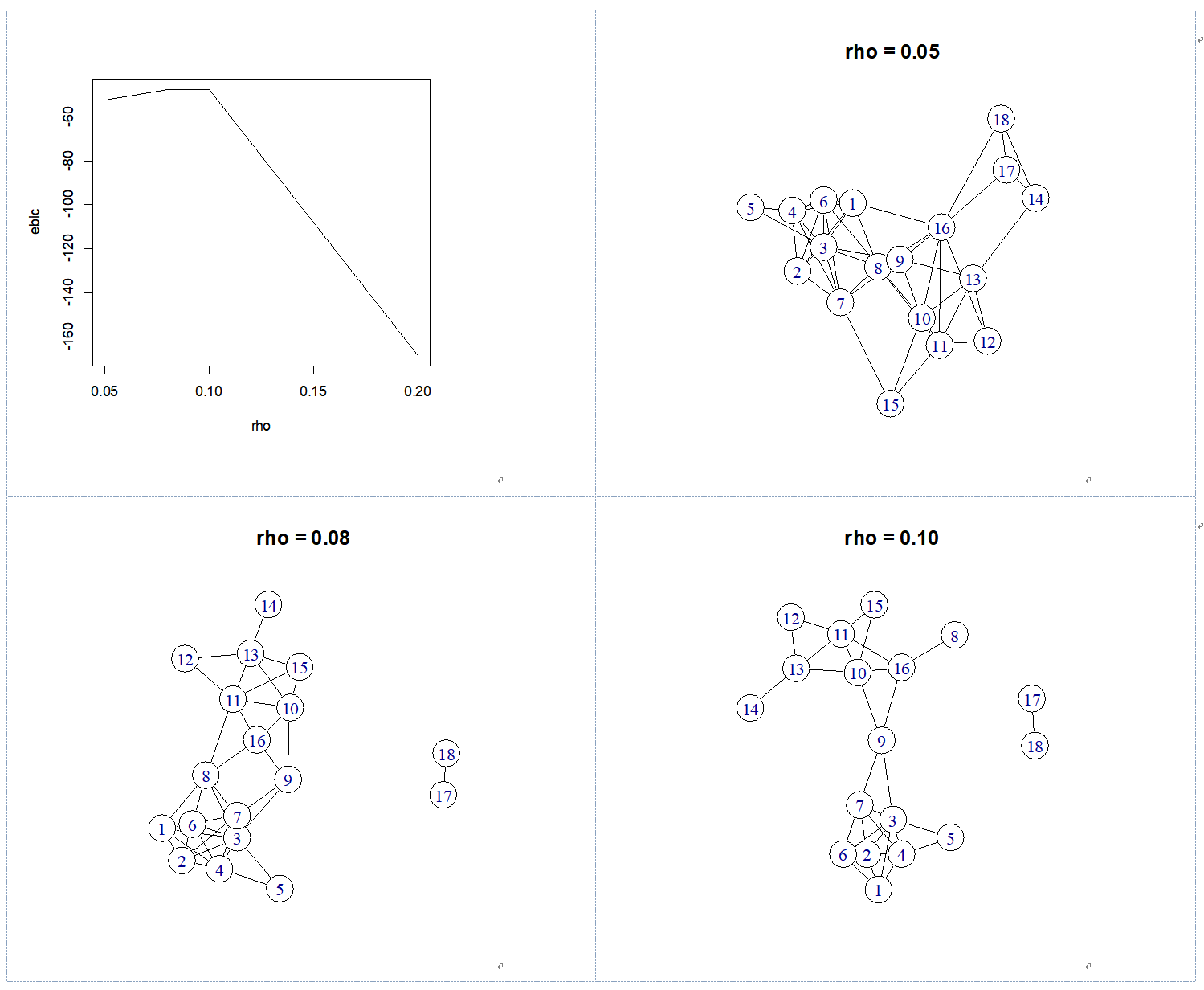
使用glasso法对这18位妇女的社会关系网络判定的结果见图一,随着罚则系数 $\rho$ 值的增大,所估计的网络密度愈加稀疏。根据eBIC法则,选择$\rho=0.1$的模型为最优模型。可以看到,图1-4区分出三个群体:编号1至7为一组,编号8和编号10至16为一组,编号17和18为第三组。编号9被判定为同时属于两个组,也就是说它承担了网桥的作用,连接两个群体。弗里曼(Freeman, 2003)汇总了21中计算方法对DGG数据进行元分析,glasso法的判定结果与这21种分析方法的绝大多数判定结果是一致的。稍微有所不同的是,glasso法单独将编号17和编号18两人判定为第三个组别,从原始数据上可以看到,她们两人仅共同出席了两次活动。在弗里曼所进行的分析中,BGR74 和OSB00 这两个方法也都将他们判定为单独的组别,在戴维斯和加纳的人类学分析中虽然将他们与编号10至16合为一组,但是将她们判定为边缘成员。由此可见,glasso法对于小群体估计也是具有敏感性的。
图1:用glasso法计算的美国南方妇女网络关联
代码如下:
# DGG 数据及示例
## 数据载入
library(igraph)
dgg<-read.csv(file = 'DGG.csv', header=TRUE)
dgg[is.na(dgg)]<-0
dgg<-t(dgg[,-1])
colnames(dgg)<-c(1:18)
dim(dgg)
dgg
## 基本 glasso 模型
library(glasso)
result = glasso(cov(dgg), rho = 0.1, penalize.diagonal=F)
# 计算偏相关系数矩阵
wi_to_pcor <- function(wi) {
p = -wi
d = 1/sqrt(diag(wi))
pcor = diag(d)%*%p%*%diag(d)
diag(pcor) = 0
colnames(pcor) <- seq_len(ncol(pcor))
pcor
}
pcor = wi_to_pcor(result$wi)
# 偏相关系数矩阵
pcor
g = graph.adjacency(pcor > 0, mode="undirected", diag = FALSE)
plot(g, vertex.color = 'white', vertex.size = 20, edge.color = 'black')
rhos <- c(0.05, 0.08, 0.1, 0.2, 0.8)
ret <- lapply(rhos, glasso, s = cov(dgg), penalize.diagonal = F)
wi <- lapply(ret, getElement, 'wi')
ret.pcor <- lapply(wi, wi_to_pcor)
ret.mat <- lapply(ret.pcor, function(x) x > 0)
ret.g <- lapply(ret.mat, graph.adjacency, mode="undirected", diag = FALSE)
for (i in seq_along(ret.g)) {
plot(ret.g[[i]], vertex.color = 'white', vertex.size = 20, edge.color = 'black', main = sprintf("rho = %.2f", rhos[i]))
}
#' @param x list of glasso result
get_ebic <- function(x, n, gamma = 0.01) {
df <- (sum(abs(x$wi) > 1e-5) - ncol(x$wi)) / 2
d <- ncol(x$wi)
-2 * x$loglik + df * log(n) + 4 * df * gamma * log(d)
}
ebic <- sapply(ret, get_ebic, n = 14, gamma = 0.1)
plot(rhos[1:4], ebic[1:4], type='l', xlab='rho', ylab='eBIC')